Dette er en rekke nyttige notater/forklaringer om funksjoner som vi har lært hittil.
Lineære funksjoner
Definisjon: y=ax+b
eksempel: y=2x+5
Lineære funksjoner kan aldri være loddrett, og er bestandig en rett linje.
I en lineær funksjon har vi noe som kalles “stigningstall” og “konstantledd”

Stigningstall er tall som forteller oss hvor mye grafen stiger hver gang vi går en x-verdi mot høyre. I bildet av grafen ovenfor kan vi se hvordan dette fungerer mer klart. Et hakk til høyre, to hakk opp.
konstantledd er verdien som forteller oss hvor grafen skjærer/passerer y-aksen. I eksemplar funksjonen vår kan vi se at 5 er i ‘b’ plassen, da skal grafen(/linjen) passere 5 på y-aksen, som vi kan se på grafen.
Proporsjonalitet
Definisjon: y=kx
eksempel: y=3x

For at en graf skal kunne klassifiseres som en proporsjonalitet må den alltid gå igjennom origo; som er skjæringspunktet til x og y aksene. 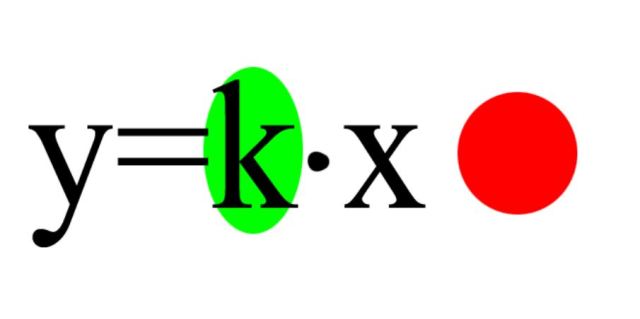
Betegnelsen for stigningstallet i proporsjonalitet definisjonen er ‘k’, men i motsetning til definisjonen for en lineær funksjon så ser vi ut til å mangle konstantleddet? Dette er altså grunnen til at proporsjonaliteten aldri forlater origo; fordi den blanke plassen der konstantleddet skal være er null, og origo er null.
Stigningstallet i eksemplet vårt er 3, og vi kan se at grafen nemlig stiger 3 hakk opp for vært hakk til høyre – akkurat som forventet.
Kvadratisk funksjon
Definisjon:
Eksempel:
